Formative Loop on campus: Carpenter Hill Elementary

The mission of Carpenter Hill Elementary School, a dynamic community of students, families, neighbors, and staff, is to empower students with the tools to succeed through nurturing relationships and innovative educational experiences.  What a great mission!  With a student population of nearly 650, this school has deep roots in its community of Hays, Texas.

Carpenter Hill has been using Formative Loop in 1st – 5th grades.  Their principal, Debbie Brown has seen sustained growth in her students.  Debbie writes, “Each of our tested grade levels (3rd through 5th) grew in Mastery from last year to this year.”

We loved reading her blog post about the students' progress through daily math practice.  You can read it in her own words here. 

Their whole campus has been engaged in the daily math practice and focusing on fixing gaps in their student knowledge.  Principal Brown shared some impressive stats with us:

  • 82% percent of 1st graders know their addition facts
  • 95% of 2nd graders know their addition facts and are working on subtraction
  • 3rd grade increased the number of students who "Mastered" (the highest status on the state STARR test) by 42%
  • 54% of their 4th and 5th grade students know ALL of their facts (addition, subtraction, multiplication, and division).
  • Their 5th grade Texas STARR scores went up 7.2% from when those students were in 4th grade

Principal Brown had this to say about the program,

“Formative loop has allowed a systematic approach in providing individualized plans for student acquisition of developmentally appropriate math skills. CHES students have demonstrated growth in basic math facts and automaticity. We have also seen a significant increase in the transfer of knowledge as young as first grade when applying new math skills to unfamiliar situations.”

We visited their campus and there is clearly a lot of passion in the staff at Carpenter Hill.  It shows in the progress their student population is making.  Here at Formative Loop, we’re proud to play a part.  Great job Carpenter Hill Colts!

Ohio class received funding from DonorsChoose.org

DonorsChoose.org makes it easy for anyone to help a classroom in need. Public school teachers from every corner of America create classroom project requests, and the community can give any amount to the project that they would like to provide.

Mrs. Kovach, a teacher at Mooney Elementary School in Cleveland, Ohio, was looking for a way to continue Formative Loop with her class.  She used the Free Trial last year and wanted to start the year off with her students.


She describes her class like this,

“We are an inner-city classroom in a large, urban district in Ohio. My class is an eclectic mix of students who are bilingual, over-age, accelerated, regular ed. and/or with special needs. Their academic abilities are as diverse as their personalities.”

We spoke to her about the process, and it’s simple:

  1. Sign up at www.donorschoose.org
  2. Learn about their "Special requests" projects (you will need to qualify first) here
  3. Work with us to get an accurate quote for your class needs
  4. Enter a compelling pitch for your classroom. You can use her excellent example here as a template: Formative Loop Doubled our Math Skills, Let's Loop Again!
  5. Reach out to local businesses who might be willing to help. Kovach received much of her funding from Staples office supplies store!

Investing in your students is a cause that many in your community might be willing to help with, and DonorsChoose makes it easy.

Mrs. Kovach sees Formative Loop as an important part of her classroom.  She says,

“The kids love the challenge and the way it is individually tailored to their level…every day the kids notice something that they learned to master from Formative Loop that helps them in class.”

Big thanks to Staples for funding the Formative Loop math program for the students of Mooney Elementary in Ohio!

The pencil is still high tech

Can you imagine a device that lets you easily communicate ideas, erase your mistakes, take anywhere, never needs charging and costs just a few cents? It's the pencil of course! We sometimes forget the magic around us. With so many digital programs out there and on the internet, in some cases students are beginning to spend the majority of their school day on a digital device. Technology is everywhere in our lives and should play a key part in our classrooms. Finding the right balance is something many schools are still struggling with. What’s the right amount of teacher/student interaction? Which skills are benefiting from digital programs? What are the drawbacks? When we set out to design Formative Loop, we immediately began with an all-digital program. We were surprised at what we found (although I am sure many of you will not be). Our goal was to make the best possible individualized math program focused on foundational skills. We knew that a daily practice was key to the success of this program. When we began testing in classrooms, it was quickly apparent that getting 20 second graders to login to a website suddenly didn't look like a quick 5-minute practice. Some schools didn't have enough devices. Even for those that had enough devices, it just didn't make sense for a quick practice since the duration of the practice was short.

Logistics aside, our second surprise was just how much magic there was to pencil and paper that our digital devices have simply not yet recreated. Children still need practice in number formation in these early years. Research was published in the journal, Learning Disability Quarterly where Virginia Berninger found that

"a keyboard doesn’t allow a child to have the same opportunity to engage the hand while forming letters…on a keyboard a letter is selected by pressing a key and is not formed…brain imaging studies with adults have shown an advantage for forming letters over selecting or viewing letters.”

Your brain works differently when putting pencil to paper! It stimulates a part of the brain called the Reticular Activating System, or the RAS. In Write It Down, Make It Happen, author Henriette Anne Klauser says that

“Writing triggers the RAS, which in turn sends a signal to the cerebral cortex: ‘Wake up! Pay attention! Don’t miss this detail!’

Amazing! This magic device in your hand, the pencil, is communicating directly with your brain and telling it to get with the program.

We have seen this in action throughout our classrooms now and believe strongly that pencil-paper has its place in math practice. It's extremely accessible compared to getting kids on computers. It provides students the mechanical practice of number formation which is critical at this age. Working through complex skills like regrouping benefit greatly. It also quickly identifies their learning gaps which allows the teacher to see their work and engage personally with that student. Long live the pencil! That is until a more magic pencil from a company like Apple is good enough and cheap enough of course.

Why students can’t problem solve if they don’t have numeracy

The goal of modern day math classrooms is to equip students to solve everyday math problems.

There are lots of approaches to developing problem solving skills. But without a foundation of numeracy, students won’t be able to reach their full problem-solving potential. Good problem solving is dependent on core numeracy skills.

In some ways, numerical fluency is like reading fluency. Both are building blocks. Reading fluency – being able to decode words – impacts reading comprehension. Many language arts teachers have observed that students with poor phonetic decoding and sight word recognition skills read so slowly that they are unable to understand the very sentence they just read.

Poor numerical fluency has the same negative effect in mathematics. When the child’s numerical ability is lacking, they struggle to solve multi-part math problems. Numerical fluency is the ability to work fluidly with numbers in a variety of mathematical situations.  Kids competent with numeracy have the ability to hold a multi-part problem in their working memory, use their skills to resolve each part, and solve the problem as a whole.

Numerate students are capable of solving multi-step math problems – and importantly – evaluating the reasonableness of the solution.  For example:

Joseph saves pictures in a 4 page photo album. He has 102 pictures in the album – 28 pictures on the first page, and 23 pictures on each of the last two pages. How many pictures are on the second page of Joseph’s photo album?

The numeracy math skills needed to solve this problem are:

  • The ability to double (or multiply by 2) – 23 x 2 = 46
  • Summing two two-digit numbers with carrying:  46 + 28 = 74
  • Subtracting with regrouping: 102 – 74 = 28
  • Evaluating the reasonableness of the solution (adding them all together to verify they sum to 102).

If your students struggle with one of these skills, they’ll be incapable – or extremely slow – to solve the problem as a whole.  Most tests these days are timed – so speed matters.

So what’s a school to do?  Be sure to put a little time into reinforcing the core numeracy skills that your students will need to draw upon to solve the problems they tackle in class.  A little investment in numeracy goes a long way.

 

Looking for a simple 5-minute a day way to do so?  You are welcome to a free trial of Formative Loop.

 

Math fluency leading to improved scores

Mina Elementary is a large public school serving the Bastrop community in central Texas.  It has over 500 students in attendance, with grades kinder through fourth.  The school has a mixed population with about 45% economically disadvantaged students.  It’s a school who clearly cares deeply about their students and community. You should see the pictures from the fall festivals, parades, and science fairs on their website!

Mina Elementary began using Formative Loop about 1.5 years ago.  Their math scores were doing well, but they had heard about other schools in the area seeing lots of success closing skill gaps through daily practice.

In the last year alone, they saw their third-grade students improve 18% on the Texas STARR test from the previous year when they were in second grade!  They also saw the number of students who were highlighted as “Mastered” by the STARR test go up 33%.  This is amazing progress in only one year.

Their principal, Reba King says,

“Formative Loop is loved by students, parents, and teachers.  Students are motivated.  Parents can easily assist with the homework and appreciate that we are putting an emphasis on holding students accountable for foundational math skills.  Teachers see the impact on student learning, and value the real-time data to drive intervention.”

Mrs. King has implemented the program campus wide in grades 1-4.  Each day, the entire school does their math practice at 7:35 am.  Once the paper-practice is complete, support staff helps enter the progress in the computer for the 3rd and 4th graders.  The other grade levels just have the teachers manage it.  They print out the next-day’s practice using the Formative Loop website.

4th Grade Teacher, Jennifer Leisure writes,

“Formative Loop is the best program I have seen to practice numeracy skills on a daily basis.  As a teacher, I can appreciate the easy implementation of Formative Loop.  The program is individualized and students go at their own pace.  It definitely has built math confidence in my students.”

Many of the grade levels include a daily homework practice from the program.  These are also individualized for each student.  Jennifer went on to say,

“I have found Formative Loop to be a powerful tool when meeting with parents in conferences.  It is easy for a parent to monitor the 5-minute nightly homework requirement and to track their child's progress through the skills.”

It’s not just the 3rd graders who saw a large improvement.  Their 1st grade population meeting their district end of year academic targets for math went up 11% and their 2nd grade population increased a total of 27% from 2015-16 to 2016-17.

We’re proud to partner with Mina Elementary.  We know student improvement doesn’t come simply from tools like Formative Loop, but also requires the dedication and skill of great teachers.  Congratulations to the students and staff of Mina Elementary on your success!

How to use gamification to make students crazy for math

I was always surprised by watching my daughter work for hours to earn a few extra virtual coins on her latest iPhone game to have enough to purchase a virtual fedora for her virtual avatar. That was of course until I noticed I found myself doing the same thing one day! It is a core part of human nature to feel validation by a clear measurement of our progress with a reward in mind.
Measurement is prevalent in the classroom. Unfortunately, the feedback can take a long time for students to receive. It can take time before a paper is returned, a test is graded, or your average grade for the quarter is given which can make the clear measure of progress a little fuzzy. What we can learn from the games we play is that the faster the feedback, the easier it is to attribute that feedback to a behavior. Formative Loop is a daily math practice. Each day we see our students getting the feedback as to whether they have passed to the next level. This in itself is a reward, and students are driven by it!
Learning from games, we have added a new points system to Formative Loop. This system gives students points for practicing their math skills (5 points) and even more for making progress (10 points when they master a skill). Each day, students will see their total points earned on the top of their practice paper.

Educators then build real-world reward programs off of these points. Having a large array of options is beneficial to the students. Here’s some typical items in the reward system:

  • 100 points – large reward (trip to the treasure box, lunch with the teacher, Hershey kiss from the principal)
  • 50 points – medium reward (line leader, shoes off day, bring a toy from home)
  • 25 points – small reward (get a sticker, choose the story to be read, choose your seat)

You may ask why we give points even when students don’t master a skill.

The reason is, we want the students to feel encouragement even for trying. This is a daily practice, not the final exam. The more engaged in practice our students are, the better the overall outcome will be.

You can also print out copies of our currency template if you want the students to practice with printed money they earn from their points.

We think this is an amazing addition to the program which will continue to build positive momentum with our students. We’d love to hear the rewards you have built around Formative Loop points. Share your stories with info@formativeloop.com!

Get ready for parent-teacher conferences with individual student reports

Having robust data to use when talking with your students' parents is always beneficial. You can show them where their student struggles and how they can support at home. Based on feedback from educators like you, we've been hard at work to improve our printable individual student report. This report will show the student's progress and how they compare to others. It will also highlight skills that they struggled with. Parents can use this report at home to reinforce skills that might still need more practice. Check it out with the instructions below and let us know what you think.

How to print a student progress report:

  1. Login to Formative Loop and click on your class
  2. Click on the student's name you wish to print a report for
  3. Click the green "Print" button

That's it! We're continuing to improve this area in the future, please let us know any changes you would like to see by sending feedback to: info@formativeloop.com

Formative Loop on campus: F W Gross Elementary

F W Gross is a medium-sized elementary school in Victoria, near the Texas gulf coast. They have around 350 K-5 students, with over 90% economically disadvantaged children. The school’s mascot is the bumblebee, and they are led by a very passionate principal, Mary Noble.

Gross Elementary began using Formative Loop in January of 2016 in grades 1-5. They were concerned about their 5th graders who were struggling with basic addition, subtraction, and multiplication skills. They wanted to help those stragglers, and begin to build up confidence in the early grade levels to solve the problem much sooner in the students’ tenure.

At the end of the 2016-17 school year, Principal Noble wrote,

“We had another AMAZING year with Formative Loop! Our teachers all agree that it is the one program we cannot live without! It has increased our benchmark scores and we have noticed our students are working problems much more efficiently.”

Each morning from 8-8:05, all of the students do their daily individualized math practice in their classroom. Math Interventionists assist the classroom teachers by going and collecting their papers at 8:06. They share space in the front office where they grade, taking about 25 minutes for the whole school. By 8:30, the interventionists are ready to return to their classroom assignments to work with students. The next day papers are printed and put into folders along with homework sheets that are utilized during that day's intervention time. Like clockwork, the teachers have data on which skills a student is stuck on and the next day’s practice ready by 8:45 am.

Mrs. Noble went on to write,

“Formative Loop has made such a difference on our campus! This program allows teachers and staff to target specific areas of need for each child. Teachers are able to utilize immediate, targeted data to pinpoint student struggles in math. Instruction is differentiated with each child working at their own pace.”

Her interventionists are scheduled to pull students throughout the school day during small groups in class. They use the Formative Loop daily report to give the teachers a quick look at the targeted needs of each student who is struggling. It helps pinpoint how they spend their time with those students.

In the 2016-17 school year, they have already seen significant progress. Their 3rd grade Texas STARR scores were up 8.6% year-to year. Their 4th-grade students increased 15.5% from when those students were in 3rd grade the previous year. Even the % of students who were designated with "Mastered" (the highest status on STARR) were up 20-30% or more in all grade levels!

We love hearing stories of student progress like this! Congratulations to the teachers and students of F W Gross Elementary. It’s your dedication and focus on improving that is making a difference.

Formative Loop Tips and Tricks

The following are the most important practices to follow for success with Formative Loop.
Commitment to practice – Make a school wide commitment to how often you plan to run the program. We recommend 4-5 days a week. The best results come from running the program daily. Weekly reporting will help you track progress. It is important that the teachers and administration all support each other in this commitment.
Intervention Plan – When students don’t pass a skill after 3 attempts, we will highlight that student as being stuck. It is important that you have an intervention plan so that these students are getting extra help to move forward.
Grading for accuracy – Some teachers will spend time checking the accuracy of every single problem. This causes them to spend too much time on what is intended to be a daily practice. We encourage spot-checking vs. checking every single problem. It has the same benefits with a lot less time.
Incentive program – Formative Loop will automatically print out award certificates for each student when they pass a major unit and track points as they practice and make progress. Students are much more engaged as they see recognition for progress. Building an incentive program is an easy way to get students begging to practice their math skills! Read more about Formative Loop Points.

Be sure to view our getting started videos to learn more about the program.

Subtraction Facts: Elementary Students’ Math Fact Nemesis

Kids learn single digit addition and multiplication facts quickly. They are helped by the commutative property of mathematics (2 + 3 = 3 + 2 and 4 x 5 = 5 x 4). If the addition or multiplication of 1’s (1 + 3 or 4 x 1) are not counted, there are only 36 discrete single digit addition and multiplication facts to learn.

Not true with subtraction facts: 8 – 5 = 3 and 8 – 3 = 5 appear as two separate subtraction facts. They are to a young student in the same fact family, but students must learn both of these subtraction facts. There is no commutative property of subtraction. To complicate matters, students must also learn double digit subtraction facts subtracting a single digit (13 – 8 = 5 and 13 – 5 = 8). Ask any elementary math teacher – the vast majority will agree. Subtraction facts are kids’ main adversary.

Is there a method to help kids to quickly learn many of their subtraction facts? Yes. There is!
Students still need to learn single digit from single digit subtraction facts (5 – 3 = 2 and 9 – 6 = 3), but those facts are much easier than single digit numbers subtracted from a double digit number (i.e. 17 – 9 = 8). There is a method that is very helpful in the latter case and adds numeracy skills of number sense and base 10 mathematics at the same time. This subtraction technique relies on student proficiency of the addition of two single digit numbers – a skill that is typically mastered well before working on subtraction facts.

This method is shown below using the math fact 15 – 7 = 8 with a typical subtraction fact format.



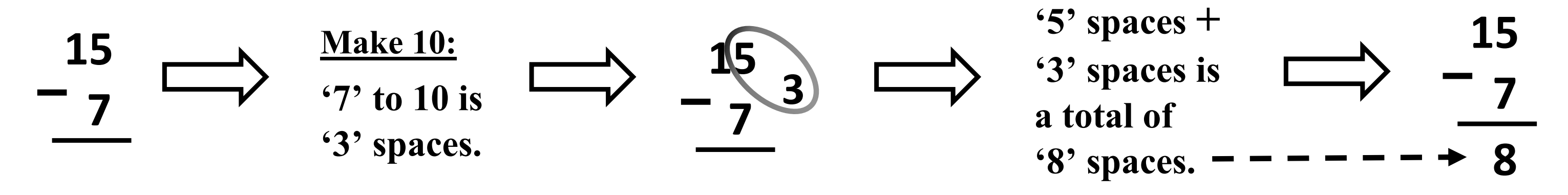
This method may appear complicated, but it has merit. After students are able to ‘Make 10’ quickly, they become very adept at the process – and subtraction facts are quickly mastered. The math skill of ‘Making 10’ should be taught to mastery prior to using this subtraction technique. Skill practice sheets for ‘Making 10’ are available in the Formative Loop Numeracy Resources Library.

Teachers should show the process on a number line so kids visually understand the physical nature of the mathematics and why this process ONLY works when subtracting a 1 digit number from a 2 digit number.

Formative Loop Parent Letter

It can be helpful to send a note to your parents about the programs their students are using on a regular basis in the classroom. We've created a template you can start from to share with your parents. Don't forget, you can also include individualized homework to send home to keep parents involved. Consider stapling this letter to their homework or as part of the student progress report!

Download the Parent Letter

Announcing Certificates of Achievement

We wanted to make you all aware of a new feature we released this week: Achievement Certificates.  When a student progresses through a skill level, we will automatically include a printed certificate you can use to recognize their achievement.  Some teachers may want to hold these to present them all at once at an assembly, or feel free to hand them out the day the student receives the award.

Here’s an example of the new certificates:
certificate
 
When the feature is enabled, you will also find a new menu item under Manage Students -> View Achievements.  This will allow you to create a certificate at any time.
 
viewachievements
 
We hope your students are motivated by the new feature!  Please share any feedback you have!